Andy Sloss' Method

This method works well with computer graphics programs.

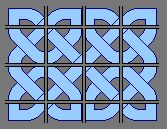
Like other methods of drawing knotwork, Andy Sloss' method starts with a grid. Instead of using the grid as a basis for the knotwork lines, Mr. Sloss simply populates each square of the grid with a pre-drawn knotwork section. Fitting the sections together like a mosaic results in the finished pattern.

Notice that the top and bottom rows of squares are half-height "end caps" that are treated differently from the body of the knotwork.

Each square in the grid has four corners (duh!), and the knotwork cord can exit the square going horizontally, vertically, or diagonally. A shorthand way of describing each square is to use a letter in each corner corresponding to the direction the cord flows in that corner.

For example:

H D D V

Note: if the upper left and lower right cord-endings don't look horizontal and vertical (respectively), that's because they aren't curved quite enough so they look a little like they're diagonal. But trust me: they're intended to be horizontal and vertical.

Once the directions of the cord endings are specified, one simply completes the cords by connecting diagonally-opposite corners, making sure that one cord goes "over" the other where they cross in the center.

Andy Sloss' book goes into a lot of detail about counting the number of possible knotwork configurations, so let's compute a simple example. There are four corners to each knotwork tile, and each corner has three possibilities (horizontal, diagonal, or vertical). Thus, there are 3 x 3 x 3 x 3 = 81 possible knotwork tiles. All 81 are drawn in the book in severals sizes and variations, including some grid-based versions which would be suitable for mapping onto computer pixels or cross stitch patterns.

Of course, these 81 tiles can not be combined at random. The cords exiting each tile must line up with cords on adjacent tiles. And cord endings at the edge of the mosaic must be turned back into the pattern, lest they dangle freely.

This method of knotwork construction is well-suited to computers. You can draw each tile once and copy or arrange them however you want in order to construct the desired pattern. It's also a good way to copy a complex knot. Simply superimpose a grid on the knot to be copied, then write out the H/D/V notation for each square in the grid and replicate it using your pre-drawn set of knotwork tiles.

For more information, get a copy of Andy Sloss' book, How to Draw Celtic Knotwork: a Practical Handbook, which is cited in my bibliography.

Visit Andy Sloss Designs.